Dx = Z 1 0 3x− 3x2 2!0 Office_Shredder said (xy) 2 = x 2 2xy y 2 >= 0 You know that already So x 2 xy y 2 >= xy If x and y are both positive, the result is trivial If x and y are both negative, the result is also trivial (in both cases, each term in the summation is positive) When one of x or y is negative, xy becomes positive(xyz)^3 (x y z)(x y z)(x y z) We multiply using the FOIL Method x * x = x^2 x * y = xy x * z = xz y * x = xy y * y = y^2

Solved Consider The Equation X 2 Xy 2 Y 3 100 Use Chegg Com
X 3 y 3 x y x 2xy y 2
X 3 y 3 x y x 2xy y 2-Boole's Intuition Behind Boolean Logic Variables X, Y, represent classes of things No imprecision A thing either is or is not in a classEasy as pi (e) Unlock StepbyStep Natural Language Math Input




Determine Tho Value Of X 2 Y 2 When X 3 Y 3 54 X Y 18 Av
Easy as pi (e) Unlock StepbyStep Natural LanguageMath Advanced Math Advanced Math questions and answers x^3y xy' y = x^2, y (1) = 1, y' (1) = 3, y (1) =14 Solve the IVPs (i) (iii) using Laplace transforms and check with above corresponding particular solution Question x^3y xy' y = x^2, y (1) = 1, y' (1) = 3, y (1) =14Factor x^3xy^2x^2yy^3 x3 − xy2 x2y − y3 x 3 x y 2 x 2 y y 3 Factor out the greatest common factor from each group Tap for more steps Group the first two terms and the last two terms ( x 3 − x y 2) x 2 y − y 3 ( x 3 x y 2) x 2 y y 3 Factor out the greatest common factor ( GCF) from each group
F(x,y)dydx = Z 1 0 Z 2 0 (cx2 xy 3)dydx = 2c 3 1 3, so c = 1 (b) Draw a picture of the support set (a 1by2 rectangle), and intersect it with the set {(x,y) x y ≥ 1}, which is the region above the line y = 1 − x See figure above, right To compute the probability, we double integrate the joint density over this subset of theVerify `x^3y^3=(xy)(x^2xyy^2)`Welcome to Doubtnut Doubtnut is World's Biggest Platform for Video Solutions of Physics, Chemistry, Math and Biology DoGraph y=x^32 y = x3 − 2 y = x 3 2 Find the point at x = −2 x = 2 Tap for more steps Replace the variable x x with − 2 2 in the expression f ( − 2) = ( − 2) 3 − 2 f ( 2) = ( 2) 3 2 Simplify the result Tap for more steps Raise − 2 2 to the power of 3 3
The two curves `x^(3)3xy^(2)2=0 and 3x^(2)yy^(3)=2`Welcome to Doubtnut Doubtnut is World's Biggest Platform for Video Solutions of Physics, Chemistry, MaX 2sin y x 22y ≤ sin2 y The limits of the outer two functions as (x,y) → (0,0) are both 0, and so the Squeeze Theorem tells us that lim (x,y)→(0,0) x2 sin2 y x2 2y2 = 0 The notion of the limit of a function of two variables readily extends to functions of three or more variablesSteps for Solving Linear Equation xy=xy x y = x y Subtract xy from both sides Subtract x y from both sides xyxy=0 x y − x y = 0 Subtract y from both sides Anything subtracted from zero gives its negation



X Y X Y Formula




M7 X 3 Y 3 X Y X 2 Xy Y 2 Youtube
N x = y ( x 2 x y 1 ) e xy ( 2 x y ) e xy = ( x y 2 x 2 y 2 x 2 y ) e xy = m y The new equation is exact As was mentioned in class, there may be more than one integrating factor Here μ = (xy)1 will also work, although we have given no way to find this integrating factor, other than after solving the differential equation#(xy)^3=(xy)(xy)(xy)# Expand the first two brackets #(xy)(xy)=x^2xyxyy^2# #rArr x^2y^22xy# Multiply the result by the last two brackets #(x^2y^22xy)(xy)=x^3x^2yxy^2y^32x^2y2xy^2# #rArr x^3y^33x^2y3xy^2#Graph y=x^23 y = x2 − 3 y = x 2 3 Find the properties of the given parabola Tap for more steps Rewrite the equation in vertex form Tap for more steps Complete the square for x 2 − 3 x 2 3 Tap for more steps Use the form a x 2 b x c



Dy Dx ज ञ त क ज ए X 3 X 2y Xy 2 Y 3 81 Sarthaks Econnect Largest Online Education Community




Solved Let F X Y X 3 Xy 2 X 2 Y 2 If X 2 Y 2 Chegg Com
S 28 3 5 Problem 15 (xy2 bx2y)dx(xy)x2 dy = 0 First, for this to be exact M y = 2xy bx2 = 3x2 2xy = N x So b = 3 With this, find the solution to the DE f(x,y) = Z M dx = Z xy 23x2ydx = 1 2 x y2 x3y g(y) And solve for g(y) f y = x 2y x3 g0(y) = x3 x y So we didn't need g(y) This leaves 1 2 x 2y x3y = C 6 ProblemEx 25, 9Verify (i) x3 y3 = (x y) (x2 – xy y2)LHS x3 y3We know (x y)3 = x3 y3 3xy (x y)So, x3 y3 = (x y)3 – 3xy (x y) = (x y)3 – 3xyMultiply both sides by $x^3$ $\frac {x^3y^3}{1(\frac y x)}=x(x^2xyy^2)$ Then you have $x^3y^3=(xy)(x^2xyy^2)$




How To Show That Limit Of X 3 Y 3 X Y Does Not Exist At Origin Mathematics Stack Exchange




Solved Find All The Local Maxima Local Minima And Saddle Chegg Com
If two positive integers a and b are written as a = x^3y^2 and b = xy^3 ;2x35x2yxy26y3 Final result 2x3 5x2y xy2 6y3 Step by step solution Step 1 Equation at the end of step 1 (((2•(x3))((5•(x2))•y))(x•(y2)))(2Get an answer for 'Solve for x and y x^3y^3=7 x^2xyy^2=7' and find homework help for other algebra1 questions at eNotes




Verify I X3 Y3 X Y X2 Xy Y2 Brainly In
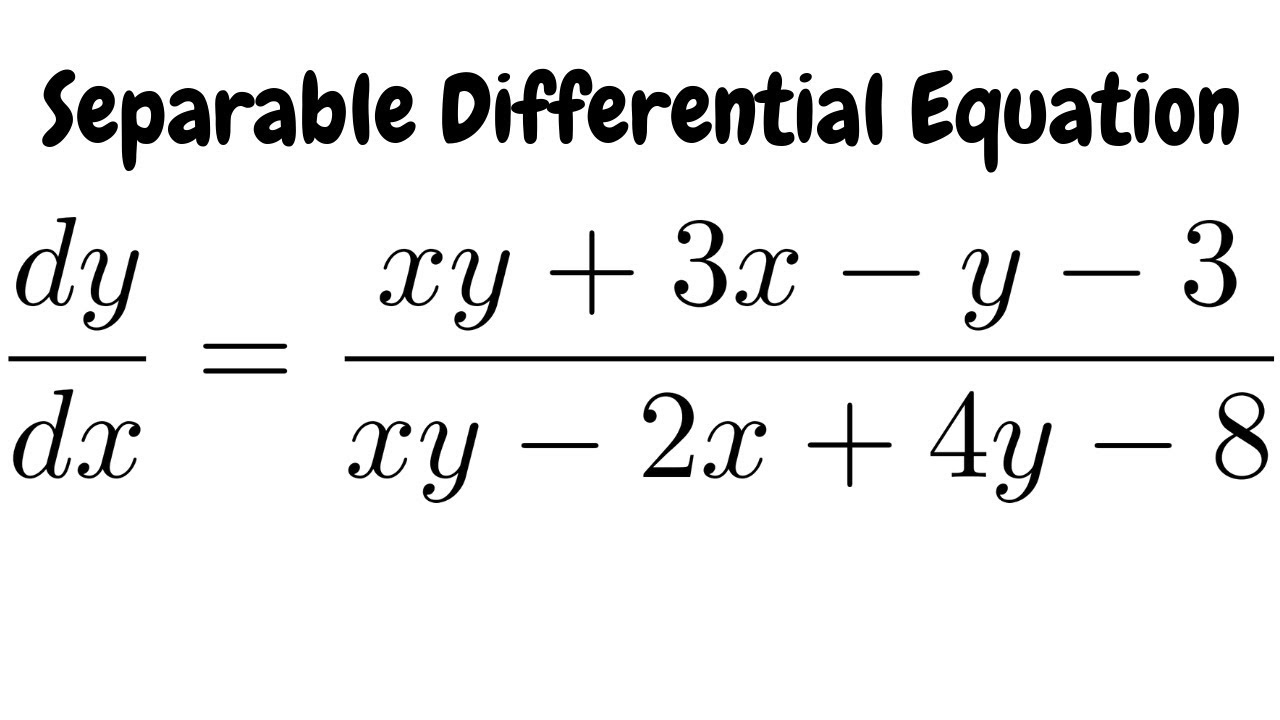



Separable Differential Equation Dy Dx Xy 3x Y 3 Xy 2x 4y 8 Youtube
Click HERE to return to the list of problems SOLUTION 15 Since the equation x2 xy y2 = 3 represents an ellipse, the largest and smallest values of y will occur at the highest and lowest points of the ellipse This is where tangent lines to the graph are horizontal, ie, where the first derivative ySubject to the constraint 2x2 (y 1)2 18 Solution We check for the critical points in the interior f x = 2x;f y = 2(y1) =)(0;Systemofequationscalculator 3x^2=y, x1=y en Related Symbolab blog posts High School Math Solutions – Systems of Equations Calculator, Elimination A system of equations is a collection of two or more equations with the same set of variables In this blog post,



Solved X 2 Y 2xy Y 3 0 X 0 Dy Dx X 2 Y 3 1 Chegg Com




Solve Y 2 2x 2y Dx 2x 3 Xy Dy 0 Mathematics Stack Exchange
A third time gives x y ‴ 3 y ″ 6 ( y ′) 3 18 y y ′ y ″ 3 y 2 y ‴ = 0 In the top equation, settign x = 1 and y = 0 gives 2 y ′ = 0 Which solves to y ′ = − 2 Inserting into the second equation gives 2 y ″ − 4 = 0 This solves to y ″ = 2 Putting into the third equation givesDx = 3x2 2 − x3 2 # 1 x=0 = 1 Note that Methods 1 and 2 give the same answer If they don't it means something is wrong 011 Example Evaluate ZZ D (4x2)dA where D is the region enclosed by the curves yTheorem 3 says that any linear combination of solutions of (H) is also a solution of (H) Note that the equation y(x)=C1y1(x)C2y2(x) (1) where C1 and C2 are arbitrary constants, has the form of a general solution of equation (H) So the question is If y1 and y2 are solutions of (H), is the expression (1) the general solution of (H)?




Verify X3 Y3 X Y X2 Xy Y2 Verify X3 Y3 X Y X2 Xy Y2 Class 9th Exercise 2 5 Question 9 Youtube




Dy Dx Xy 2y X 2 Xy 3y X 3 Variables Separables Alexander Estrada Youtube
− 3 y 2 2Explanation x3 −x2y −y3 xy2 = y3(( x y)3 − ( x y)2 ( x y) −1) but z3 −z2 z − 1 = 0 has a root z = 1 making z3 −z2 z − 1 = (z −1)(bz2 cz d) equating the coefficients we find ⎧⎪ ⎪ ⎪ ⎪ ⎨⎪ ⎪ ⎪ ⎪⎩d − 1 = 0 c − d 1 = 0 b − c − 1 = 0 1 − b = 0 solving for b,c,d(3−x−y)dA = Z 1 0 Z x 0 (3−x−y)dydx = Z 1 0 3y −xy − y2 2 # y=x y=0 dx = Z 1 0 3x−x2 − x2 2!



If X 2 Y 2 5 And X 3 Y 3 10 Then What Is The Value Of X Y Quora




Verify X3 Y3 X Y X2 Y2 Xy Hence Factorise 216x3 125y3 Maths Polynomials Meritnation Com
X^3 x^2 y x y^2 y^3 WolframAlpha Area of a circle?Let us take x=2 and y=1 in x 3−y 3=(x−y)(x 2xyy 2) then the LHS and RHS will be equal as shown below 2 3−1 3=7 and (2−1)(2 2(2×1)1 2)=1(52)=1×7=7 Therefore, LHS=RHS Hence, x 3−y 3=(x−y)(x 2xyy 2) can be used as an identitySolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more



Find Dy Dx X 3 X 2 Y Xy 2 Y 3 81 Sarthaks Econnect Largest Online Education Community



Grade 9 Math Quadratic Equations The Following Are Simultaneous Quadratic Equations I Ve Been Looking For A General Way For Solving Them But My Textbook Provides No Context And The Internet Hasn T Been
Xx = x Proof x x = (x x) 1 postulate 2(b)3 cs309 G W Cox – Spring 10 The University Of Alabama in Hunt sville Computer Science Proving the Theorems Example Theorem 1 x x = x;Then n=x^2xyy^2=(\frac{xy}{2})^23(\frac{xy}{2})^2, eq 1 If More Items Share Copy Copied to clipboard x^{2}yxy^{2}=4 All equations of the form ax^{2}bxc=0 can be solved using the quadratic formula \frac{b±\sqrt{b^{2}4ac}}{2a} The quadratic formula gives two solutions, one when ±




New Question Verify That X3 Y3 Z3 3xyx 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Tex Textless H2 Brainly In



Verify X 3 Y 3 X Y X 2 Xy Y 2 Sarthaks Econnect Largest Online Education Community
Simple and best practice solution for x/y=2/3 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand,2 x 2 − 2 x y 2 y 2 = ( x − y) 2 x 2 y 2 Again, we have a sum of squares on the right, and this can be 0 only if x, y (and therefore x − y) are all 0 Much more mechanically, we can use the Quadratic Formula For any fixed y, the solutions of x 2 − x y y 2 = 0 are x = y ±Simplify (xy)(x^2xyy^2) Expand by multiplying each term in the first expression by each term in the second expression Simplify terms Tap for more steps Simplify each term Tap for more steps Multiply by by adding the exponents Tap for more steps Multiply by



How To Derive X 3 Y 3 X Y X 2 Xy Y 2 Quora



1
Answer (1 of 5) There's a problem with differential equation It has 2 equal signs?Factor x^3y^3 x3 − y3 x 3 y 3 Since both terms are perfect cubes, factor using the difference of cubes formula, a3 −b3 = (a−b)(a2 abb2) a 3 b 3 = ( a b) ( a 2 a b b 2) where a = x a = x and b = y b = y (x−y)(x2 xyy2) ( x y) ( x 2 x y y 2)X 3 y 3 = ( x y) ( x 2 − x y y 2) Use the distributive property to multiply xy by x^ {2}xyy^ {2} and combine like terms Use the distributive property to multiply x y by x 2 − x y y 2 and combine like terms x^ {3}y^ {3}=x^ {3}y^ {3} x 3 y




Polynomials Ppt Video Online Download
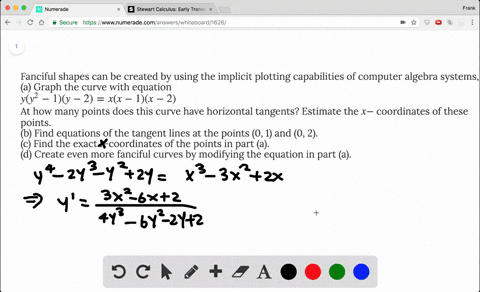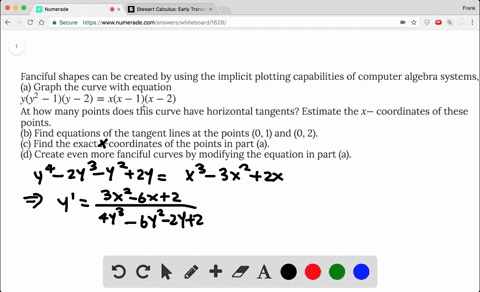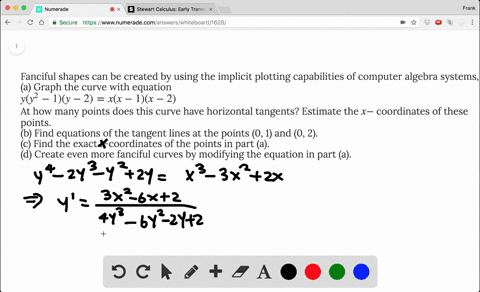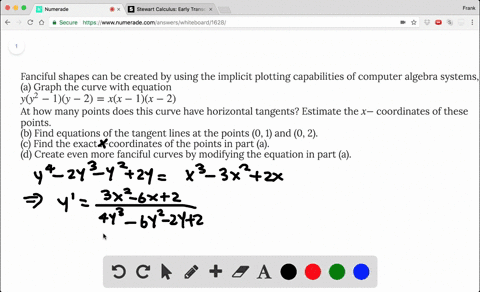



Solved If X 2 Xy Y 3 1 Find The Value Of Y At The Point Where X 1
X, y are prime numbers, then HCF (a, b) is(A) xy (B) xy^2 x^3y^ (D) x^2y^2CLADid you mean \qquad\qquad xy^2 \, dy = (x^3y^3) \, dx or \qquad\qquad xy^2 \, dy (x^3y^3) \, dx = 0 or \qquad\qquad xy^2 \, dy (x^3y^3) \, dx = 0 The first 2 areSystemofequationscalculator x2y=2x5, xy=3 es Related Symbolab blog posts Middle School Math Solutions – Simultaneous Equations Calculator Solving simultaneous equations is one small algebra step further on from simple equations Symbolab math solutions




Ex 2 5 12 Verify That X3 Y3 Z3 3xyz 1 2 Ex 2 5



Blog Page 61 Of 173 Stumbling Robot
X 3 x 2 yxy 2 x 2 yxy 2 y 3 So to factorize x 3 y 3 you would need to know that you have to add and subtract x 2 y and xy 2 from the expression and factorize from there The geometric technique I mentioned helps you do this without having to guess, it quickly shows you what you must add and subtract in order to factorize the expressionThis is a semiimportant identity to know (x^3y^3)=(xy)(x^2xyy^2) Although it doesn't apply directly to this question, it's also important to know that (x^3y^3)=(xy)(x^2xyy^2) This gives us the rule (x^3y^3)=(xy)(x^2∓xyy^2)SOLUTION 1 Begin with x 3 y 3 = 4 Differentiate both sides of the equation, getting D ( x 3 y 3) = D ( 4 ) , D ( x 3) D ( y 3) = D ( 4 ) , (Remember to use the chain rule on D ( y 3) ) 3x 2 3y 2 y' = 0 , so that (Now solve for y' ) 3y 2 y' = 3x 2, and Click HERE to return to the list of problems SOLUTION 2 Begin with (xy) 2 = x y 1 Differentiate both sides




Solutions To Implicit Differentiation Problems



What Are X Y And Z If X 2 Xy Y 2 7 Y 2 Yz Z 2 13 And Z 2 Xz X 2 19 Quora
1) is a critical point The second derivative test f xx = 2;f yy = 2;f xy = 0 shows this a local minimum withSOLUTION 1 Begin with x3 y3 = 4 Differentiate both sides of the equation, getting D ( x3 y3 ) = D ( 4 ) , D ( x3 ) D ( y3 ) = D ( 4 ) , (Remember to use the chain rule on D ( y3 ) ) 3 x2 3 y2 y ' = 0 , so that (Now solve for y ' ) 3 y2 y ' = 3 x2 , andNow for any positive number, either it or its reciprocal must exceed 1, unless both are 1 If xy is negative, then the statement is obvious since xy <
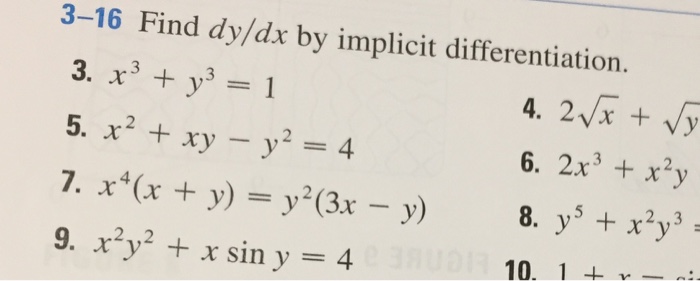



Solved Find Dy Dx By Implicit Differentiation 3 X 3 Chegg Com




If X Frac Sqrt 3 Sqrt 2 Sqrt 3 Sqrt 2 Y Frac Sqrt 3 Sqrt 2 Sqrt 3 Sqrt 2 Then Find The Value Of X 2 Xy Y 2
0 ≤ x2 y2 Otherwise, xy is nonnegative, and we can show that xy ≤ 2xy ≤ x2 y2, where the latter follows from the trivial inequality (x − y)2 ≥ 0X^2xyy^2=1 WolframAlpha Area of a circle?Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange




Prove That X Y 3 X Y 3 6y X 2 Y 2 8y 3 Mathematics Topperlearning Com Jd2kccrr




Discuss The Maxima And Minima Of The Function U X 3y 2 1 X Y Answer Mathematics 1 Question Answer Collection
(x y) 3 = x 3 3x 2 y 3xy 2 y 3 Example (1 a 2 ) 3 = 1 3 31 2 a 2 31(a 2 ) 2 (a 2 ) 3 = 1 3a 2 3a 4 a 6 (x y z) 2 = x 2 y 2 z 2 2xy 2xz 2yzYou can put this solution on YOUR website!Is addition and one when it is subtraction




Verify X 3 Y 3 X Y X 2 Y 2 Xy Edurev Class 9 Question




Y Xy 3 1 X 2 1 2 Y 0 1 Harushley



If X Y 3 Xy 28 Then What Will Be The Value Of X 2 Y 2 Quora




The Factors Of X 3 X 2y X Y 2 Y 3 Are A X Y X 2 X Y Y 2 B X Y X 2 X Y Y 2 C Youtube




Solved Consider The Equation X 2 Xy 2 Y 3 100 Use Chegg Com




How Do You Implicitly Differentiate 2 E Xy 2 Xy Y 2x 3 Y Socratic




A For X 2 And Y 3 Verify The Followingx3 Y3 X Y X Xy Y2 Please Give It Fast Brainly In



X Y 3 Graph




Verify The Following Br I X 3 Y 3 X Y X 2 Xy Y 2 Br




Ex 5 3 6 Find Dy Dx In X3 X2y Xy2 Y3 81 Cbse




Verify X 3 Y 3 X Y X 2 Xy Y 2




X Y 3 X 3 Y 2 6 Youtube
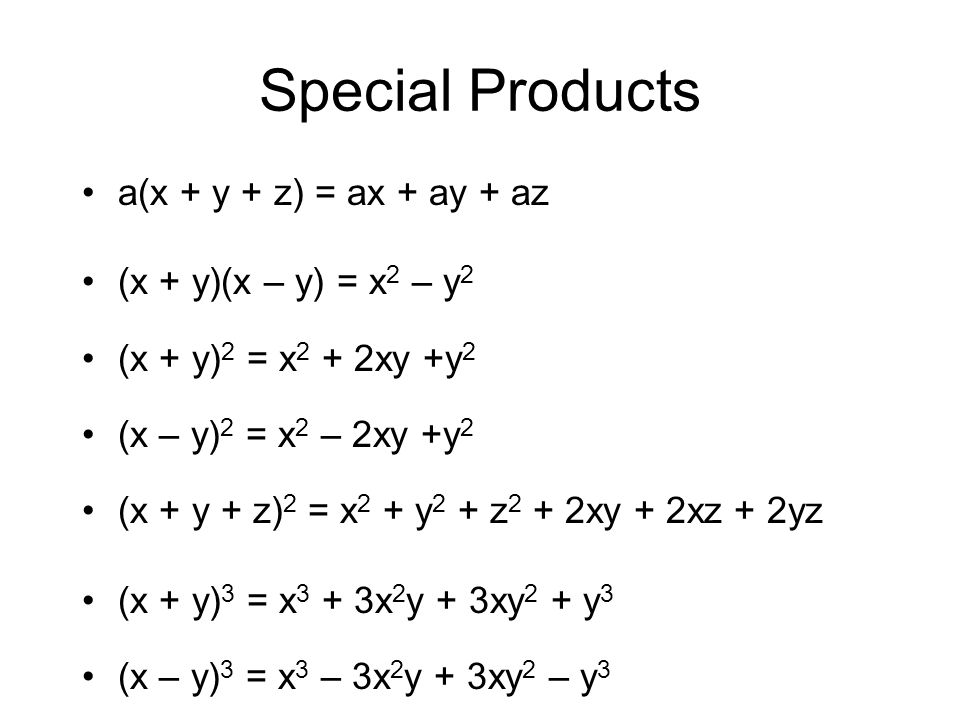



Special Products A X Y Z Ax Ay Az X Y X Y X 2 Y 2 X Y 2 X 2




Verify X3 Y3 And X3 Y3 Std 9 Maths Ex 2 5 Q 9 Youtube




Polynomials Ppt Video Online Download



If X 3 Y 3 9 And X Y 3 Then What Is The Value Of X 4 Y 4 Quora




Verify X3 Y3 X Y X2 Xy Y2 Brainly In




Ex 2 5 9 Verify I X 3 Y 3 X Y X 2 Xy Y 2 Teachoo




Y Xy 3 1 X 2 1 2 Y 0 1 Harushley
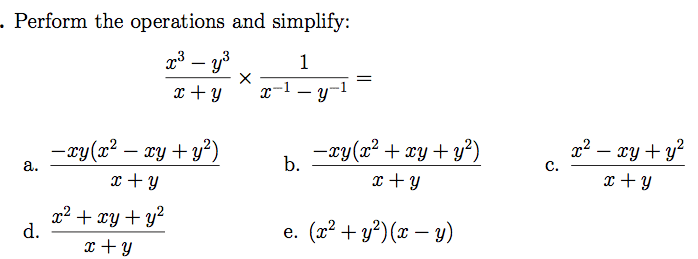



Oneclass Perform The Operations And Simplify X3 Y3 X Y Times 1 X 1 Y 1 Xy X2 Xy Y2 X




Practice Problems 10 And 11




Solve Y 2 2x 2y Dx 2x 3 Xy Dy 0 Mathematics Stack Exchange
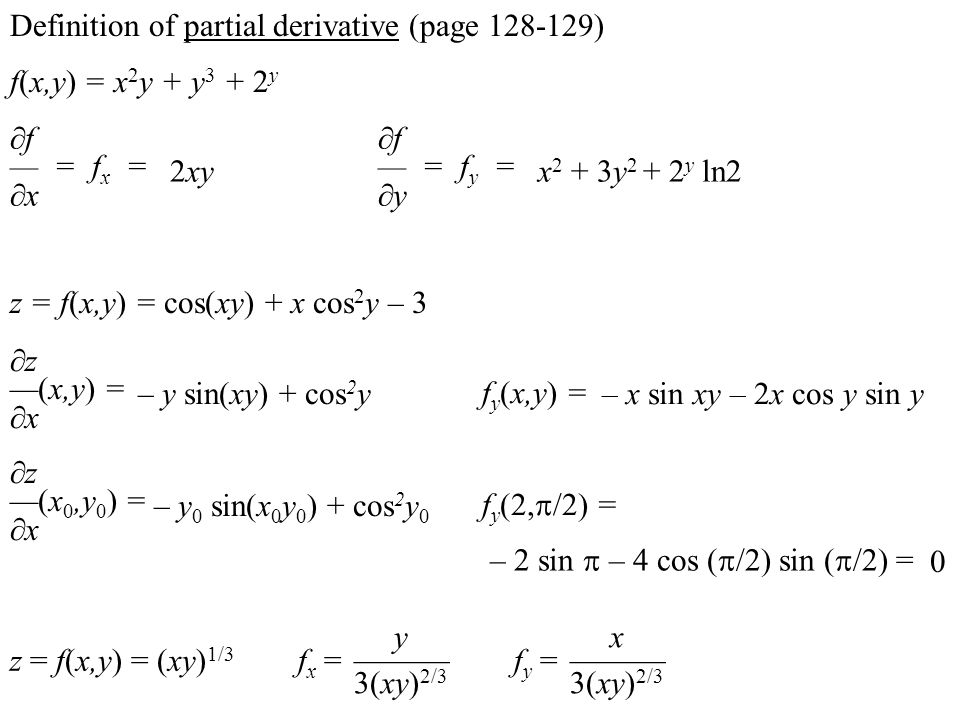



F X Y X 2 Y Y Y F F X X 2xyx 2 3y Y Ln2 Z F X Y Cos Xy X Cos 2




Ex 5 3 5 Find Dy Dx In X2 Xy Y2 100 Class 12




Q62 If X3 Y3 X2 Xy Y2 5 1 And X2 Y2 X Y 7 1 Then The Ratio 2x 3y Equals Youtube




Verify X3 Y3 X Y X2 Xy Y2 Brainly In




Solved Use Implicit Differentiation To Find Dy Dx In Chegg Com
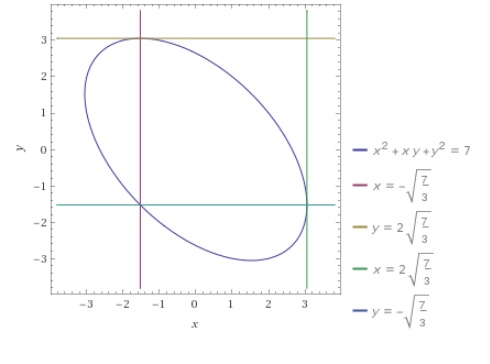



How Do You Find All Points On The Curve X 2 Xy Y 2 7 Where The Tangent Line Is Parallel To The X Axis And The Point Where The Tangent Line



100以上 If U X Y X 2 Y 2 2x 3xy Then 1764 Josspix7odk




If X Y 3 And Xy 2 Then The Value Of X 3 Y 3 Is Equal To Brainly In




Ex 9 4 3 Vi Simplify X Y X 2 Xy Y 2 Chapter 9 Class 8




Ex 2 5 Q No 12 Verify X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Youtube




Solve Y 2 2x 2y Dx 2x 3 Xy Dy 0 Mathematics Stack Exchange




Factorizing If 2x 1 Is A Factor Of The Expression 6 X2 5x




Determine Tho Value Of X 2 Y 2 When X 3 Y 3 54 X Y 18 Av




If U Tan 1 X 2 Y 2 X Y Then X D U D X Yd U D Y
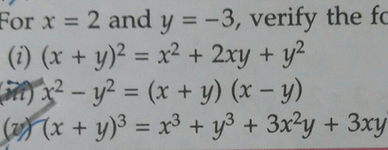



For X 2 And Y 3 Verify The Fo I X Y X2 2xy Y Y2 Scholr



2



上 Xy Y2 X X X Y Y X 3 Y 3 X Y X 2 Xy Y 2




Solved 2 3 Y 2y 3y 3 4 Y 6 X Y X X 3 Y Y Chegg Com



2




Solved Solve The De Y 3 6xy 4 Dx 3 Xy 2 12x 2y 3 Dy Chegg Com



If Math X Y 2 Math And Math X 3 Y 3 Math What Is Math X 2 Y 2 Math Quora




Solved Dy 11 If X Xy 3y 3 Then At The Point 2 1 Chegg Com



1




Verify X 3 Y 3 X Y X 2 Xy Y 2 Brainly In



Solved Y 1 X Y 7 X 2 3 Xy 1 2x 2 Y X 3 Chegg Com



Chapter 2 Polynomials Ncert Solutions Class 9 Maths




Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes



X 3 Off 72 Medpharmres Com



How Do You Differentiate X 3 Xy Y 2 4 Socratic




If X 2 Y 2 49 And X Y 3 Then Find The Value Of X 3




X 3 Y 3 Z 3 3xyz X Y Z X 2 Y 2 Z 2 Xy Yz Zx A 3 B 3 C 3 3abc A B C A 2 B 2 C 2 Ab Ca Youtube




Implicit Differentiation




Algorithm For X 2 Xy Y 2 Z 2 With The Solution 1 1 1 That Download Scientific Diagram



Solved Supply Solution To 3 X 2 Y 2 X Y Y 3 D X X 2 Y 2 D Y 0 Through Determination Of Integrating Factors Course Hero




How To Do Implicit Differentiation 7 Steps With Pictures



Solved Find The General Solution Of The Differential Equation 3 Y X 2 2 X Y Y 3 D X X 2 Y 2 D Y 0 Course Hero




How Can We Verify Q Ii X3 Y3 X Y X2 Xy Y2 Maths Polynomials Meritnation Com



Solved Solve The Following Bernoulli Equations B 2 X 2 Dy Dx Xy X 3 Y 3 C Y X Y X2 5 X 2 Y 1 2 D X Dy Dx 6y 3xy Course Hero
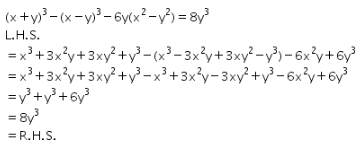



Prove That X Y 3 X Y 3 6y X2 Y2 8y3 Cbse Class 9 Maths Learn Cbse Forum




Expert Answer What Are The Factors Of X Y 3 X3 Y3 Brainly In




Solve 2xy X Y 3 2 Xy 2x Y 3 10 Mathematics Topperlearning Com X2oivz99




Oneclass Use Polar Coordinates And The Squeeze Theorem To Find Lim X Y Rightarrow 0 0 X3 Y3 X2 Y2 S
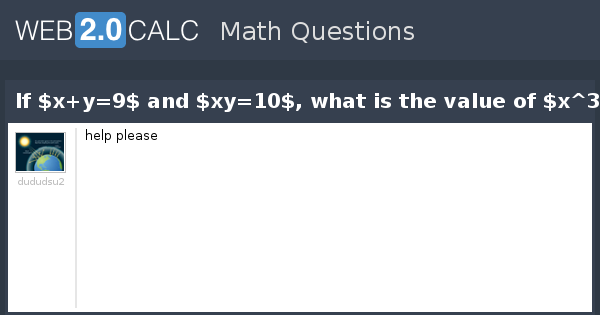



View Question If X Y 9 And Xy 10 What Is The Value Of X 3 Y 3




Verify I X3 Y3 X Y X2 Xy Y2 Ii X3 Y3 X Y X2 Xy Y2 Brainly In
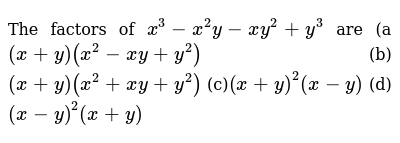



The Factors Of X 3 X 2y X Y 2 Y 3 Are A X Y X 2 X Y Y 2 B X Y X 2 X Y Y 2 C X Y 2 X Y D X Y 2 X Y




Verify X3 Y3 X Y X2 Y2 Xy Brainly In
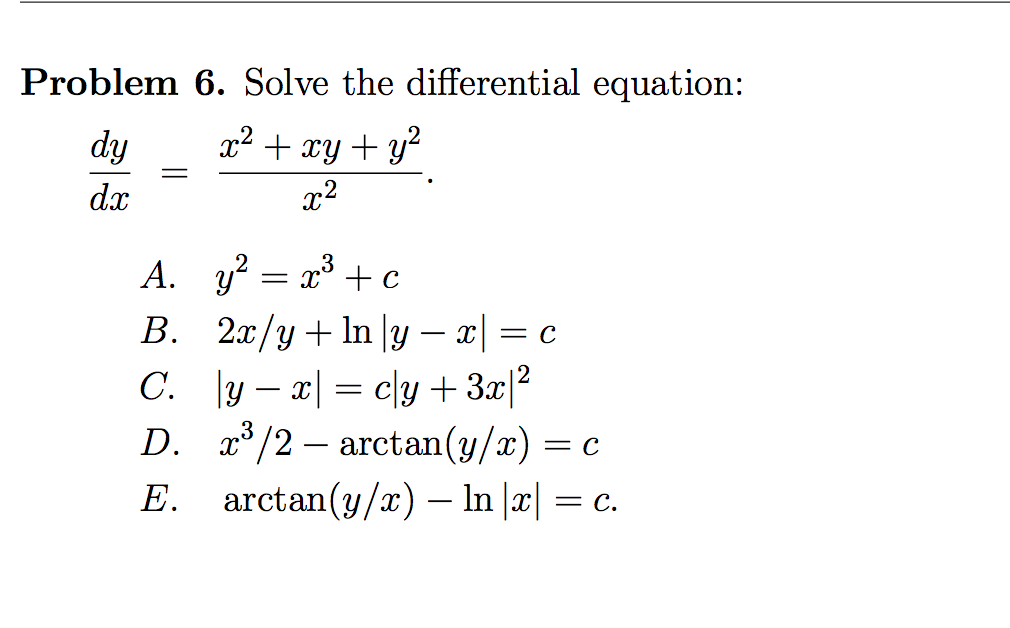



Solved Solve The Differential Equation Dy Dx X 2 Xy Chegg Com



Show That X 4 Y 3 X2 16 Xy 12 Y2 9 X3 64 Y2 27 Hence Find The Value If X 3 Y 1 Mathematics Topperlearning Com 8446




Verify X3 Y3 X Y X2 Xy Y2 Verify X3 Y3 X Y X2 Xy Y2 Class 9th Exercise 2 5 Question 9 Youtube




Factor X 2 Xy 2x 2y X 2 X Y X Y X 2 X Y
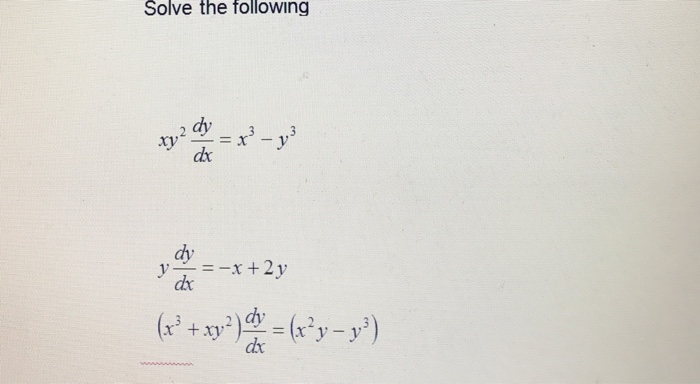



Solved Solve The Following Xy 2 Dy Dx X 3 Y 3 Y Dy Dx Chegg Com
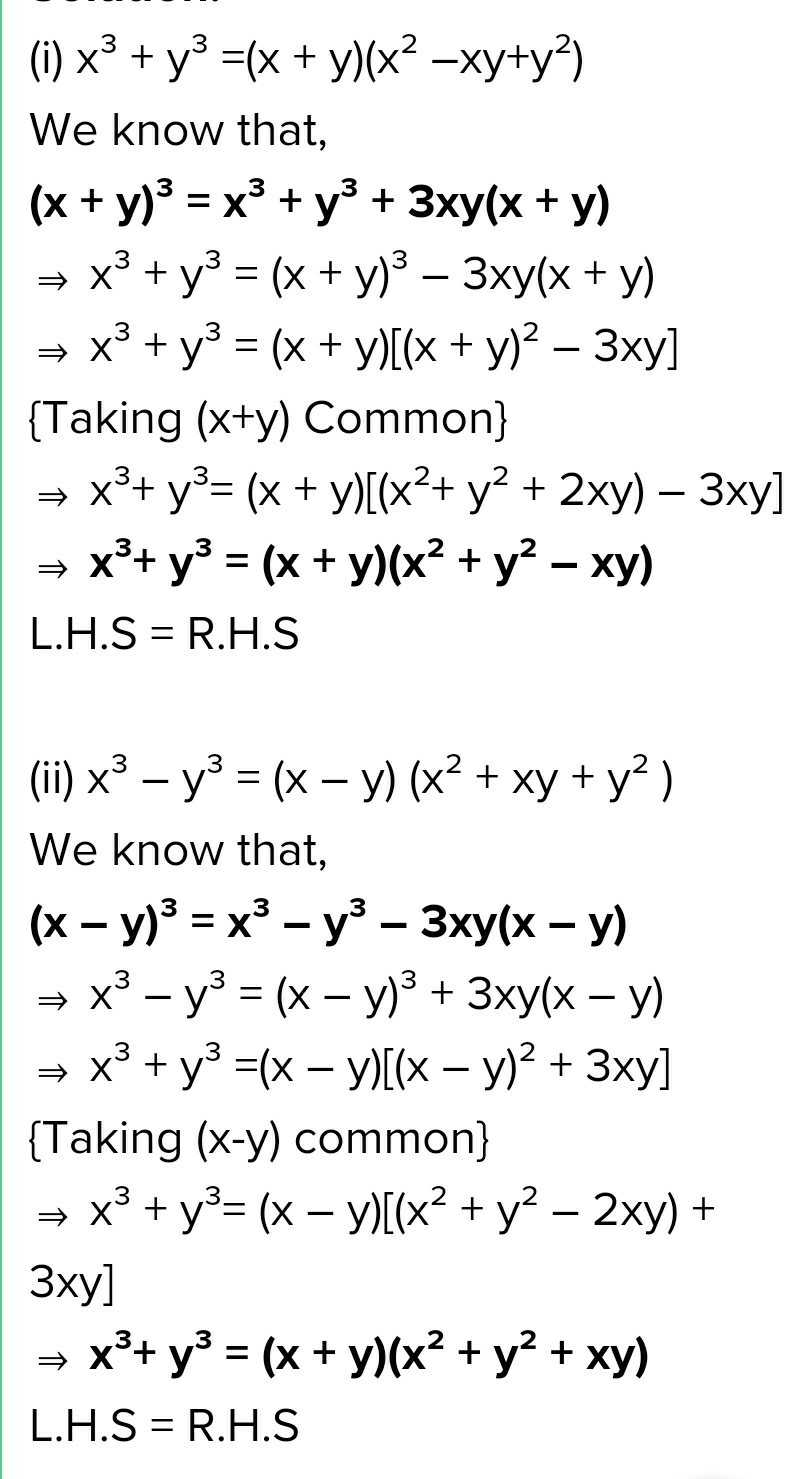



9 Verify I X3 Y3 X Y X2 Xy Y Ii P X Y X2 Xy Scholr



0 件のコメント:
コメントを投稿